Types of Functions

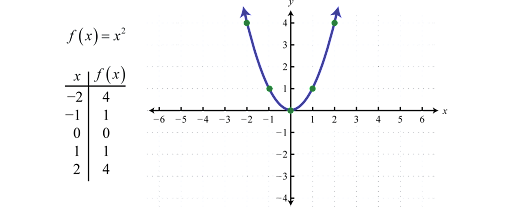
A function is a mathematical equation which can define to represent a quantity. It can written as a sum, a product, or a difference. There are various types of functions, including multivalued functions, function from X to s, and functions with regularity.

Multivalued functions

Multivalued functions are functions whose input is two or more values. They usually referred to as correspondences, point-to-set maps, or multimaps. Because of this, they distinguished from everyday functions such as the logarithm or the trigonometric power function. Although the term may seem unfamiliar, it is used in a variety of contexts, and is not to confused with multivariate functions or the inverse of a single-valued function.

A simple example of a multivalued function is the function f:B=A. For a given independent variable x, f(a) is equal to f(b) if and only if f(a) is equal to b. In other words, f:B=A has a branch point at 0 that connects the first two branches of f. There are also several other common ways of defining multivalued functions.

One way is to consider a multivalued function as an inverse of a non-injective function. In this case, the function is not reversible. The inverses of the function do not preserve all of the information that the original function did. However, in general, a multivalued function has a partial inverse of the function that it derives from. Another common way to define a multivalued function is by assuming that the function has analytic continuation along a closed path. This means that the multivalued function has a value change at some point after it analyzed. Depending on the particular form of the function, the value can vary considerably.

A more general way to study multivalued functions is by applying regularity properties. This involves perturbation theory for convex inequalities and continuity of convex functions. When the ranges of the function have internal points, multivalued functions exhibit desirable regularity properties.

Several examples of these include the arctangent function, which has imaginary units as its branch points. The nth root of arctan(x) has a branch point. It is also possible to define a multivalued function by applying the implicit function theorem.

Similarly, multivalued functions can arise as a result of analytic continuation. As discussed in Section 2.4, these functions have two or more branch points and are discontinuous along curves. Alternatively, they can define as the nth root of a function that has a multi-valued explicit root.

Multivalued functions can also defined in terms of a principal value. For instance, a bijective function idA on A has an absolute identity. Likewise, the multivalued holomorphic function on a punctured disc has a ring structure.

A further way of describing a multivalued function is by using a multivalued partial function. The multivalued partial function from A to B also known as Rf from A to B. Both the f:A-B and f*:A=B have multivalued partial functions that associated with a particular domain. Hence, the multivalued partial function from A to B has a multivalued inverse function.

Functions from X to s

Functions from X to s are a class of mathematical operations that assign a set of elements in one set to an element in another. In mathematics, these operations can be either continuous or discrete. One example of a discrete function is the natural logarithm, a bijective function that takes positive real numbers and turns them into real numbers. Similarly, the exponential function maps real numbers onto positive numbers.

Besides arithmetic, functions also defined in other ways. One such way is the bar chart, which is often used to define functions whose domain is a finite set. Another is the formula, which describes a combination of functions that previously defined. The most common type of function is the identity function. This is a function that assigns every element of a set X to an element of a set Y. It is frequently denoted by the symbol g.

A more complicated function is the function f:X – Y, which assigns every element of a set Y to an element of a set X. Another is the inverse function g f:X – Y, a function that gives back the same element of Y but returns a different element of X. Those functions that not a direct assignment of Y to X called surjection and injection. Often, a function’s most interesting properties can reformulated in a language of relations.

There are many different kinds of functions, ranging from a sequence of natural numbers to a set of arithmetic operations. Some authors have divided them into the different classes and made a distinction between functions and maps. Other authors use the term functions interchangeably. However, it is important to distinguish between the two.

First, a function is a mapping from a set of things to another set. For example, the function f:P(A)-N is a map of a subset of the set A to a subset of the set N. Likewise, the function k:R-R is a function that maps a subset of the set X to a subset of the set R. But the functions that really count are the one to one and the one to many.

Among the best known functions are the exponential function, the inverse of the exponential function, and the formula describing a combination of arithmetic operations. Generally, it is difficult to examine an image of such a function unless it has a large number of elements. Nevertheless, a function whose elements are small is still useful. If a function has more than n elements, it is usually impossible to check its function signature.

The most important function from X to s is the formula f (X, Y) – s, which assigns elements from X to elements of Y. In the context of arithmetic, it is a function that uses all the elements of Y, which is a function – or a map – that is one to one.

Functions with regularity

Regularity in functions is a topic of interest to mathematicians. The definition of regularity depends on the application. However, in the context of numerical computation, the regularity of a function is an essential condition to achieve uniform convergence of a numerical scheme. In order to determine the best numerical schemes for solving a variety of real world problems, a comprehensive understanding of the properties of regularity is a must. Specifically, the regularity of the test function is a vital ingredient to the success of a numerical method.

Aside from the aforementioned test function, there are many other factors that need to be taken into consideration. For example, the speed of convergence is critical to the accuracy of a numerical approximation. To accomplish this, the correct set of bounded measurable test functions is required. Also, the appropriate use of derivatives is crucial. This is especially true in the case of weakly bounded test functions. Moreover, there are a number of other factors to consider, including the size of the singular set and the scalability of the problem. Consequently, the optimal order of a given test function may not be the same as the best order of a given solution.

Besides, in the context of a finite dimensional system, the standard discretization schemes are dominated by space-time white noise. Hence, in order to reduce the order of convergent subproblems, we need to consider more realistic assumptions. Such an approach would provide better rates of convergence. One could also generalize the finite dimensional approach by incorporating a more comprehensive class of non-regular test functions. Fortunately, it’s not too hard to do.

A regularity aficionado can easily identify the most pertinent and practical facets of a good regularity theorem. The best way to do this is to begin by applying the aforementioned Koebe theorem to the real world problem of a quaternion centered on the square of the x-y plane. Then, use the aforementioned tangent cone analysis to refine the preliminary results. It is then time to take the next step and introduce a more robust model. This requires introducing stronger singularities.

Finally, there are other relevant and interesting factors to be considered. For instance, the smoothness of the function and mappings is a crucial metric to measure. But, while the smoothness of a function is important, the most impressive property is the preservation of its smoothness under certain operations. Thus, it is a reasonable hypothesis that a finite dimensional formulation of the Kolmogorov equation can lead to the emergence of a measurable regularization effect. Likewise, it is expected that a generalization of the finite dimensional approach to an infinite dimensional problem could yield the same result.

Other than the aforementioned f-O(n), there are other notable regularity theorems. Some of the more noteworthy ones include the Central Limit Theorem, the e-regularity theorem, the Lebesgue scalability theorem and the shortest possible path of a truncated cylinder.Party